Action-Angle Networks

Physics Insight

There is a subclass of Hamiltonian systems called Liouville integrable systems.
The Liouville-Arnold theorem guarantees that, for these systems, there exists a canonical transformation to a set of coordinates called Action-Angle coordinates, with which the phase space is greatly simplified and allowing for easier prediction.

The Architecture

Daigavane et al.¹ introduce Action-Angle networks, an architecture that takes advantage of the linear evolution of the angle variable for Liouville-Arnold theorem to evolve the system forward in time.

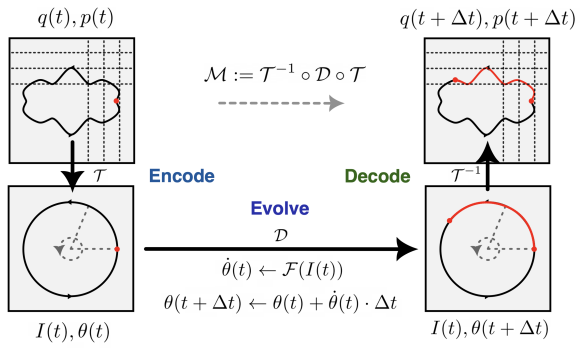
The paper adopts an autoencoder-type architecture:

• Encode step: they use a GSympNet² network to do the canonical transformation from $(q(t), p(t))$ to $(I(t), \theta (t))$,
• Evolve step: they take advantage of the fact that the angle coordinate evolves linearly with time to use the Euler update rule to get $\theta (t + \Delta t)$*, and
• Decode step: they use the inverse of the GSympNet network to go back to position-momentum at the new time step
  N.B.: GSympNets are very easily invertible by just reserving order of the gradient modules and negating their learnable parameters. For more details, check again²

*: the $\dot{\theta} (t)$ (used in the Euler update rule in the evolve step) is approximated using a multi-layer perceptron.

This is the schematic of the architecture (image taken from the paper¹):

The loss function of the action-angle network has the following two terms:

• $L_{\text{predict}} = \frac{1}{1 + \Delta t} \sum_{t_0 \in \text{Tr}} ||\mathcal{M} (u(t_0), \Delta t) - u(t_0 + \Delta t)||^2$, and
• $L_{\text{action}} = \frac{1}{T} \left (\hat{I} (t_0) - \frac{1}{T} \sum_{t_0 \in \text{Tr}} \hat{I}(t_0) \right)$ (this term is to enforce the constancy of the action variable),
  where $\text{Tr}$ is the training data composed of position $q(t)$ and momentum $p(t)$ data for a number of time steps.